設定

中心極限定理（Central Limit Theorem）とは，母集団が（分散をもつ）どのような分布であったとしても， サンプル分布との誤差は，サンプルサイズを大きくしたとき，近似的に正規分布に従う，というものである。

以下では，二項分布からのサンプルを用いて，中心極限定理の例示を行う。

N <- 5000 # 試行回数
max.n <- 50 # サンプルサイズ
p <- 0.2 #確率

データと枠の準備

−4から4まで0.01刻みの等差数列をseq()で作成し，xseqに代入する。 vec.for.meansにNAを5000個入れる。 par()は，全てのグラフィックスパラメータの現在値がリストとして得られる。 mfrow = c(m,n)は，画面がm行n列からなる複数の図表に分割される。ここでは2列に並べるという命令である。

xseq <- seq(-4, 4, by = 0.01)
vec.for.means <- rep(NA, N) 
par(mfrow=c(1,2))

シミュレーション

シミュレーションを行う。 二項分布からサンプルを取り出すにはrbinom()を用いる。 ここでrbinom(1,n,p)/nは，
$$ p(x) = \binom{n}{x} p^x (1-p)^{n-x} $$
を意味する。つまり，以下のシミュレーションは， 表がでる確率0.2のコインをn回ふって，表が出た回数投げた回数で割ることで，表が出た割合を求める，という試行を5000回繰り返し，表が出た割合のデータを5000個作っている。

二項分布B(50, 0.2)から，

for (n in 1:max.n) {
    # 1から50回まで繰り返す 1から5000回まで繰り返す
    for (i in 1:N) {
        vec.for.means[i] <- rbinom(1, n, p)/n  # 当りが出た割合
    }
}

作図

上で作成したデータを正規化する。
$$ std.x = \frac{\bar x - p}{\sqrt{n p (1- p)}} $$

std.means <- sqrt(n) * (vec.for.means - p) / sqrt( p * (1 - p)) #正規化

作図する。

plot.ecdf(
  std.means,
  xlab="Standardized Sample Mean",
  xlim=c(-4,4),
  ylab="CDF F(x)",
  main=paste("CDF for Sample Means n=",n,sep="")
  )
abline(v=-1,col="green")
points(xseq, pnorm(xseq), type="l", col="red")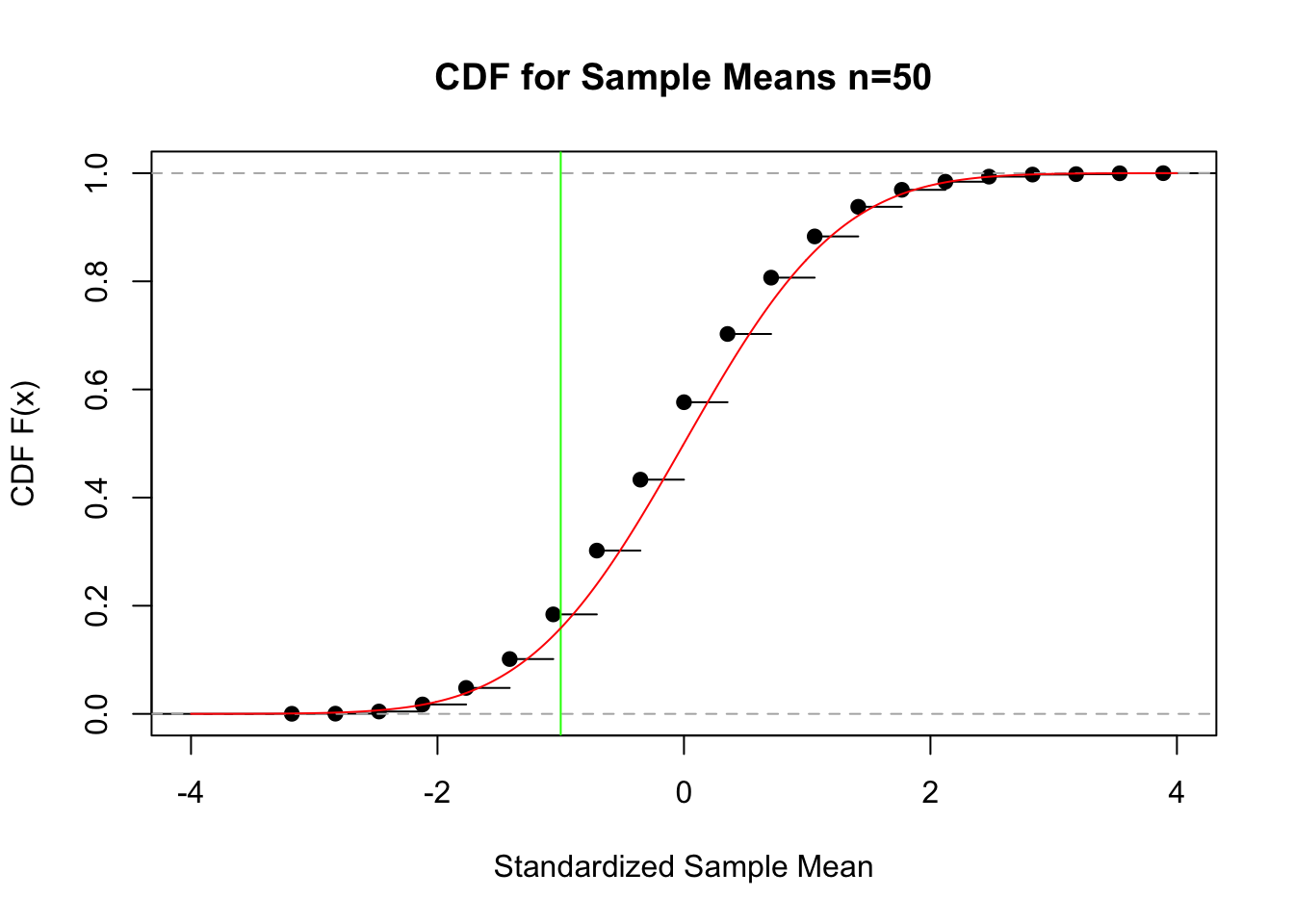

breakseq <- sqrt(n) * (seq(-0.5, (n + 0.5), length.out = (n + 2)) / n-p ) / sqrt(p * (1 - p))
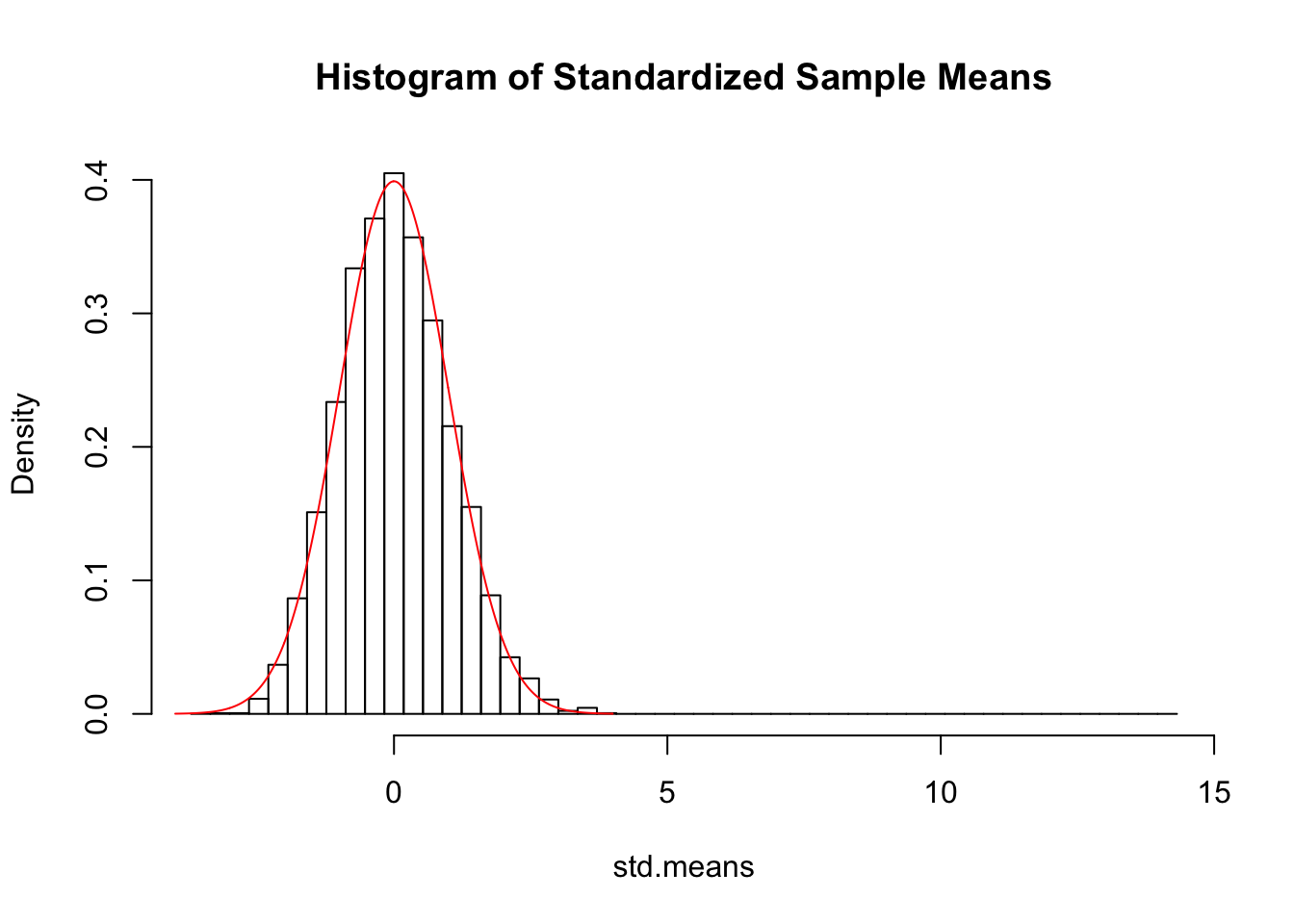
hist(std.means,
     prob=TRUE,
     main="Histogram of Standardized Sample Means",
     breaks=breakseq
     )
points(xseq,
       dnorm(xseq),
       type="l",
       col="red"
       )

use_vec <- scan("", what = character(), nmax = 1, quiet = TRUE)